How Consumers Decide I
A framework for analyzing decisions
The core ingredients: Acts, States, and Outcomes
- {\(A_i\)} = The set of acts: the options that a decision maker must choose between
- {\(S_j\)} = The set of states: the various possible ways in which the world might turn out.
- {\(O_{ij}\)} = The set of outcomes: the different possible consequences of each act given each possible state
Acts, states, and outcomes
Example: Decision problem = Should you have a barbecue in the park on May 20?
- {\(A_i\)} = {\(A_1\) (have a barbecue), \(A_2\)(eat indoors)}
- {\(S_j\)} = {\(S_1\) (sunny day), \(S_2\)(rainy day)}
- {\(O_{ij}\)} = {\(O_{11}\) (a sunny barbecue), \(O_{12}\) (a wet barbecue), \(O_{21}\) (a meal indoors while it is sunny), \(O_{22}\) (a meal indoors while it rains)}
Decision Matrix




Sunny Rainy Barbecue Indoor
Decision Matrix
| Sunny | Rainy | |
|---|---|---|
| Barbecue | \(O_{11}\) | \(O_{12}\) |
| Indoor | \(O_{21}\) | \(O_{22}\) |
Utilities
| Sunny | Rainy | |
|---|---|---|
| Barbecue | 100 | 0 |
| Indoor | 30 | 50 |
Utilities and probabilities
| Sunny (.5) | Rainy (.5) | |
|---|---|---|
| Barbecue | 100 | 0 |
| Indoor | 30 | 50 |
Maximizing expected utility
\[EU(A_i) = \sum U(O_{ij}) \times P(S_j)\]
The expected utility of having a barbecue (\(A_1\)) is:
- \(EU(A_1) = U(O_{11}) \times P(S_1) + U(O_{12}) \times P(S_2)\)
- \(EU(A_1) = (100 \times .5) + (0 \times .5) = 50\)
The expected utility of not having a barbecue (\(A_2\)) is:
- \(EU(A_2) = U(O_{21}) \times P(S_1) + U(O_{22}) \times P(S_2)\)
- \(EU(A_2) = (30 \times .5) + (50 \times .5) = 40\)
MEU recommendation: Have a barbecue
Status of EUT
- A normative model of decision making tells us how people ought to make decisions. A descriptive model tells us how people actually do make decisions.
- MEU is often presented as a normative model, but fails as a descriptive model. So, how do people actually make choices?
Prospect Theory

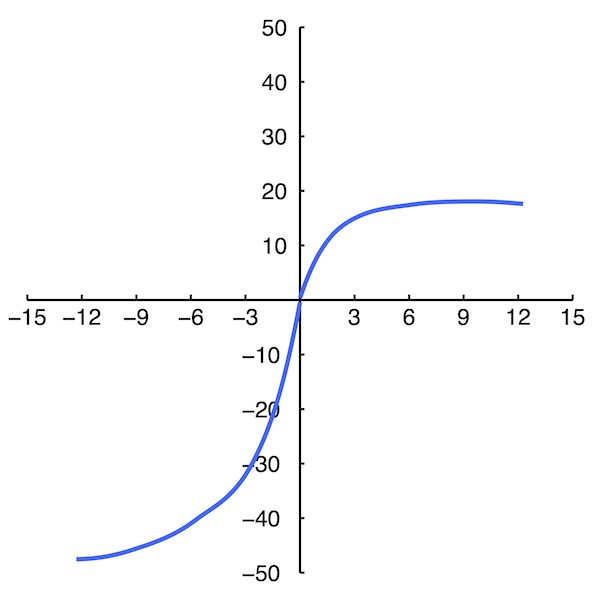
Prospect Theory
Value
Outcome
Prospect Theory
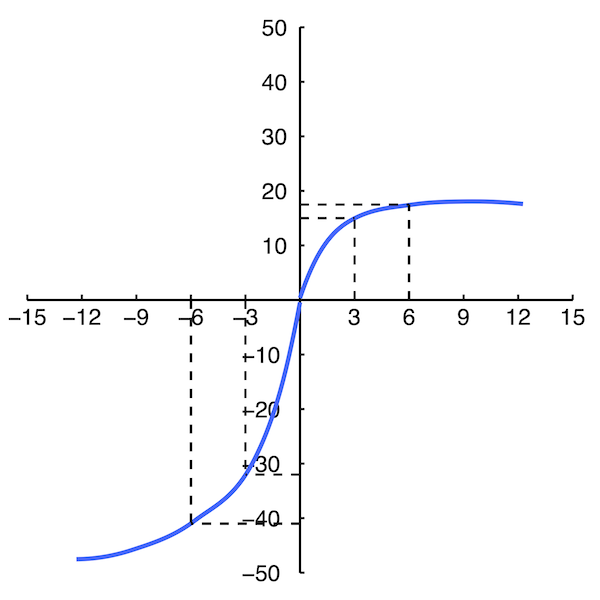
The value function
- Diminishing sensitivity
- Reference dependence
- Loss aversion
Decision weights
- Overweighting small probabilities
- Underweighting medium and large probabilities
- Extreme behaviour close to 0 or 1
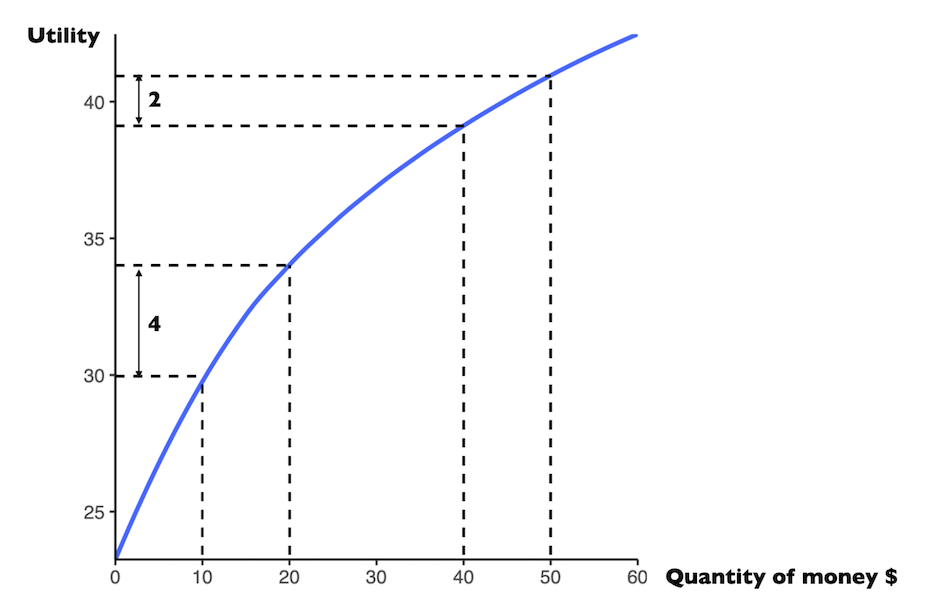
Expected Utility
The value function of PT
Value
Outcome
The isolation effect
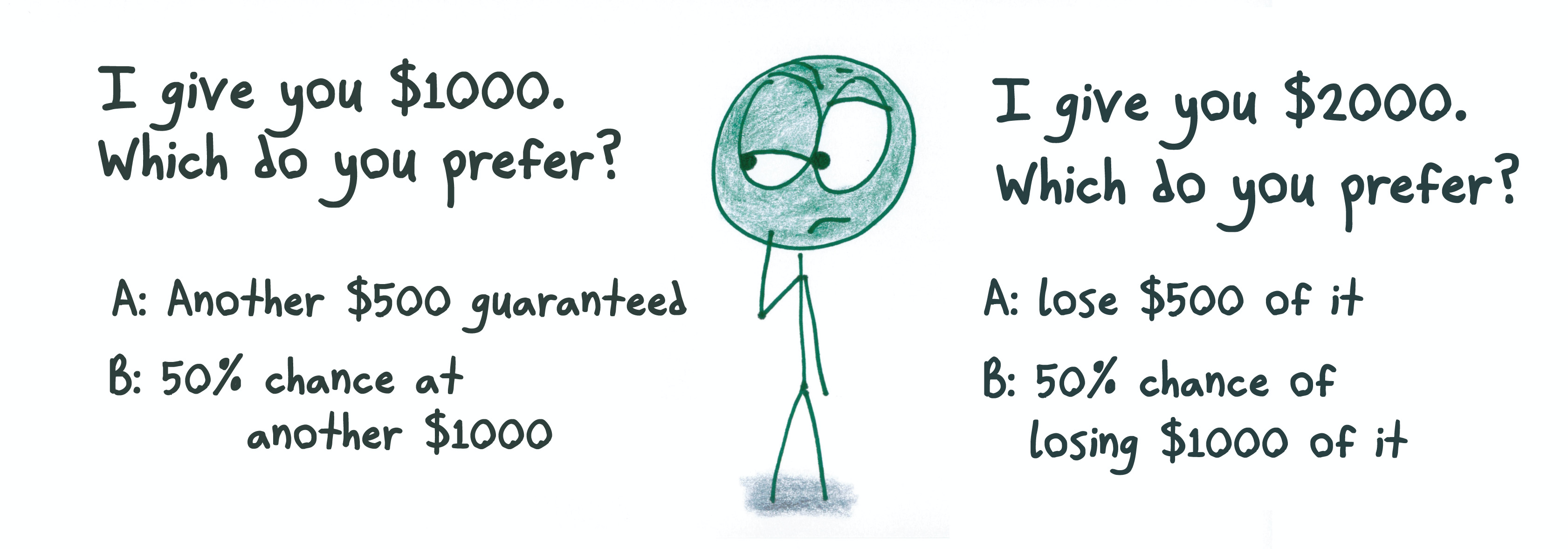
Framing
Imagine that Canada is preparing for the outbreak of an unusual disease, which is expected to kill 600 people. Two alternative programs to combat the disease have been proposed. Which of the following two programs you would favour?
- If Program A is adopted, 200 people will be saved.
- If Program B is adopted, there is a one-third probability that 600 will be saved and a two-thirds probability that no people will be saved.
Loss as opposed to gain version:
- If Program C is adopted, 400 people will die.
- If Program D is adopted, there is a one-third probability that nobody will die and a two-thirds probability that 600 people will die.
Risk aversion in the gains domain

Risk seeking in the loss domain

Loss aversion
Suppose I offered you a gamble in which I flip a fair coin and you call it in the air. If you’re right, you win $10, but if you’re wrong, you lose $10.
Would you play?
What does the minimum winning amount need to be for you to accept the gamble? (you still lose $10 if you are wrong)
The endowment effect
Once people acquire something, they become reluctant to give up, even when offered a price they would not have paid for the object in the first place.

Sellers = $7 Choosers = $3
The endowment effect
The fourfold pattern
| Gains | Losses | |
| Small probabilities | Risk-seeking | Risk-aversion |
| Medium and large probabilities | Risk-aversion | Risk-seeking |
Decision Weights
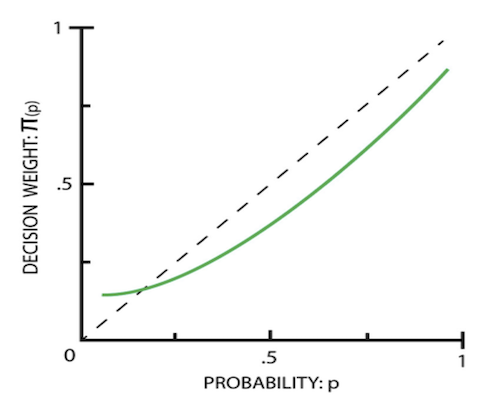
Decision makers transform the objective probability of an outcome into a decision weight.
- Overweighting of small probabilities
- Underweighting of moderate and large probabilities
- Extreme behaviour close to zero and one
Small probabilities
Problem 1. Choose between:
- 0.001 chance of winning $1,000
- winning $1 for sure
Problem 2. Choose between:
- 0.001 chance of losing $1,000
- losing $1 for sure
The certainty effect
People place special emphasis on outcomes that are guaranteed to occur or guaranteed not to occur.
Consider a game of Russian roulette.
- How much would you pay to reduce the number of bullets from 1 to zero?
- How much would you pay to reduce the number of bullets from 4 to 3?
A shift from uncertainty to certainty is weighted more than an equivalent shift from one uncertain state to another.
Deal or no deal
- Go to: https://www.gamenora.com/game/deal-or-no-deal/
- Read the rules
- Start the game
- During each round, after the appropriate number of cases has been opened, calculate the expected value of the remaining cases (add the values left in play and divide by the number of unopened cases)
- Record the banker’s offer, expected value of the unopened cases, and your decision for each round
Mental accounting
People categorize money and resources according to their source and intended use, and often treat those categorized funds differently. One dollar is no longer equivalent to another.
Mental accounting
You are on your way to the theatre. In your wallet, you have a ticket for which you paid $20, and a $20 bill. When you arrive at the theatre, you discover that you have somehow lost the ticket.
Would you spend your remaining $20 on a ticket?


Mental accounting
You are on your way to the theatre. In your wallet, you have two $20 bills. When you arrive at the theatre, you discover that you have somehow lost one of the bills.
Would you spend your remaining $20 on a ticket?


Non-fungibility of money
You want to buy a car stereo. The dealer near your house sells it for $200, but if you drive across town, you can get it for $100. Would you drive to get 50% off (saving $100)?



Non-fungibility of money
You want to buy a car with a stereo. The dealer near your house sells it for $41,000, but if you drive across town, you can get it for $40,900. Would you drive to get .002% off (saving $100)?



Mental accounting
100 coupons worth $.64 each  One coupon buys one roll of dice. If total is 9 or more, get 5 coupons to cash in
One coupon buys one roll of dice. If total is 9 or more, get 5 coupons to cash in




Group 1: 1 envelop of 100 coupons
Group 2: 4 envelops of 25 coupons
Group 3: 10 envelop of 10 coupons
Mental accounting
100 coupons worth $.64 each  One coupon buys one roll of dice. If total is 9 or more, get 5 coupons to cash in
One coupon buys one roll of dice. If total is 9 or more, get 5 coupons to cash in




Played on average 43 coupons
Played on average 25.5 coupons
Played on average 16 coupons
Diminishing sensitivity
Scenario 1: Mr. A wins two small lotteries in one day, one for $50.00 and one for $25.00. Mr. B wins one lottery for $75.00. Who do you think would be happier?
Scenario 2: Mr. A received a letter from the IRS saying that he owes $100.00. On the same day, he received a letter from the state tax authority informing him that he owes $50.00. Mr. B received a single letter from the IRS telling him that he owes $150.00. Who do you think would be more upset?
Combining mental accounting and prospect theory
When we have two gain or loss experiences, we experience the steepest part of the curve — the part closest to the origin – twice
- We feel two wins more positively than one win
- And more negatively with two losses than one
Recommendation: Segregate gains and combine losses
Coupling pain and benefit
Mr. A and Mr. B both joined health clubs. Mr. A’s club charged a fixed fee for each month of usage, payable at the end of the month. Mr. B’s club charged an hourly fee for using the health club, with the total payable at the end of the month. By chance, both men used the health club about the same amount, and both ended up getting a bill for the same amount at the end of the month. Who enjoyed himself more while at the health club?
- Mr. A
- Mr. B
- The same
48% 14% 38%
Topics for the term project
- Augmented reality in marketing
- Scarcity marketing
- Social media influencers
- Guerilla marketing
- Neuromarketing
- Retro marketing
- Artificial intelligence in marketing
- Loyalty reward programs
- Green marketing
- Behavioural targeting
